Explicit Methods

Precondition Explicit

Therewith an ordinary differential equation can be solved, it is necessary, that it is writable in explicit form:

Given $f$, a function of $x$, $y$, and derivatives of $y$. Then an equation of the form

$$ f ( x , y , y′ , \dots, y^{ (n − 1) } ) = y^{(n)} $$

is called an explicit ordinary differential equation of order $n$.

Dormand Prince

Example

$$ \begin{pmatrix} y_{1} \\ y_{2} \\ y_{3} \\ \end{pmatrix}^{’} = \begin{pmatrix} (I_{2} - I_{3})/I_{1} y_{2} y_{3} \\ (I_{3} - I_{1})/I_{2} y_{3} y_{1} \\ (I_{1} - I_{2})/I_{3} y_{1} y_{2} + f(x) \\ \end{pmatrix} $$ $$ f(x) = \begin{cases} 0.25 sin^2(x) & if 3\pi \leq x \leq 4 \pi \\ 0 & otherwise \\ \end{cases} $$

We choose the constants and initial condition as:

$$ I_{1} = 0.5, I_{2} = 2, I_{3} = 3, i_{1}(0) = 1.0, i_{2}(0) = 0.0, i_{3}(0) = 0.9 $$

and solve the initial value problem in the interval $t \in [0, 20.0]$

pub struct Euler<T>
{
	i1: T,
	i2: T,
	i3: T,

	time_span: (T, T),
	init_cond: Vector<T>
}


impl<T> Default for Euler<T>
	where T: Real
{
	fn default() -> Euler<T> {
		Euler
		{
			i1: T::from_f64(0.5),
			i2: T::from_f64(2.0),
			i3: T::from_f64(3.0),
			time_span: (T::from_f64(0.0), T::from_f64(20.0)),
			init_cond: vector![T::from_f64(1.0); T::from_f64(0.0); T::from_f64(0.9)]
		}
	}
}

impl<T> ExplicitODE<T> for Euler<T>
	where T: Real
{
   	fn func(self: &Self, x: &T, y: &Vector<T>) -> Vector<T> {
		let y_1s: T = ((self.i2 - self.i3) / self.i1) * (*y.get(1) * *y.get(2));
		let y_2s: T = ((self.i3 - self.i1) / self.i2) * (*y.get(2) * *y.get(0));

		let f: T;
		if *x >= T::from_f64(3.0) * T::pi() && *x <= T::from_f64(4.0) * T::pi()
		{
			f = T::from_f64(0.25) * x.sin() * x.sin();
		}
		else
		{
			f = T::zero();
		}
		let y_3s: T = ((self.i1 - self.i2) / self.i3) * (*y.get(0) * *y.get(1)) + f;
		return vector![y_1s; y_2s; y_3s];
	}

    fn time_span(self: &Self) -> (T, T) {
		return self.time_span;
	}

    fn init_cond(self: &Self) -> Vector<T> {
		return self.init_cond.clone();
	}
}

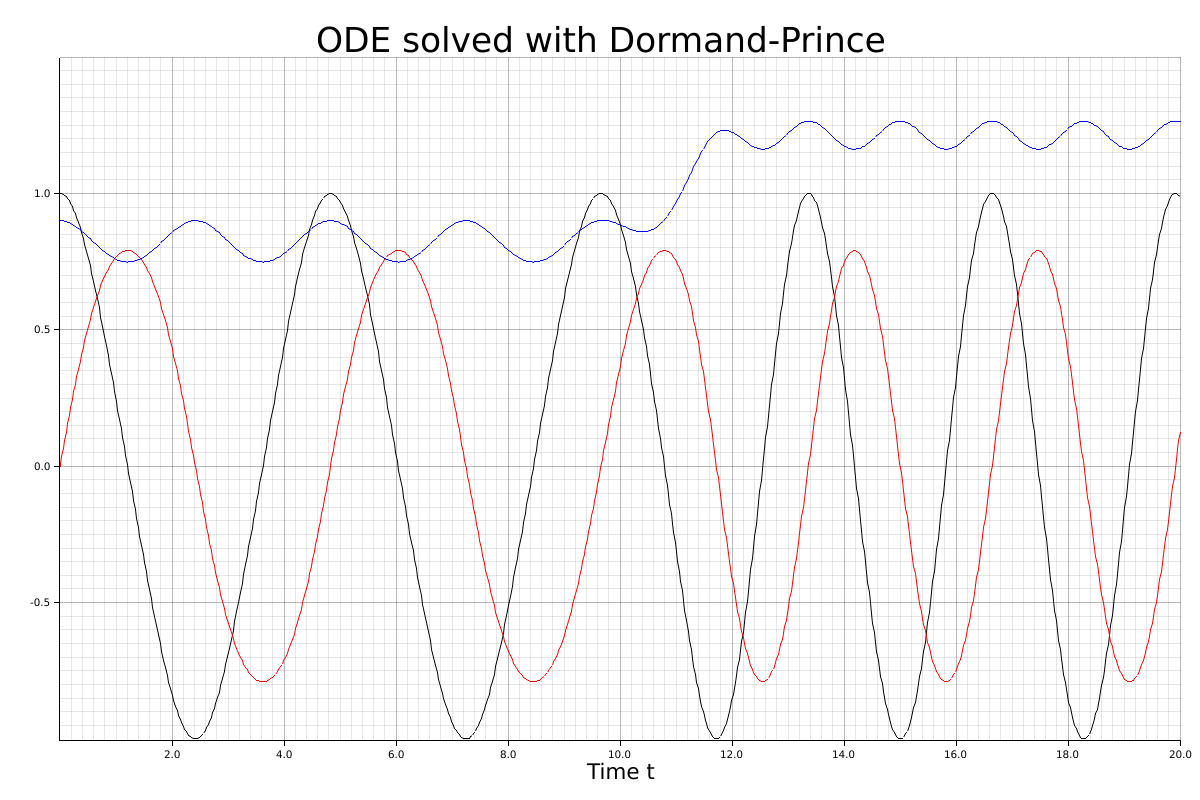
Now we solve this ODE with the Dormand-Prince method:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77


use mathru::{
    algebra::linear::vector::Vector,
    analysis::differential_equation::ordinary::{
        problem::Euler,
        solver::explicit::runge_kutta::adaptive::{DormandPrince54, ProportionalControl},
        ExplicitInitialValueProblemBuilder,
    },
    vector,
};
use plotters::prelude::*;

fn main() {
    let x_start: f64 = 0.0;
    let x_end: f64 = 20.0;

    // Create an ODE instance
    let explicit_euler = Euler::default();
    let problem = ExplicitInitialValueProblemBuilder::<f64, Euler<f64>>::new(
        &explicit_euler,
        x_start,
        vector![1.0; 0.0; 0.9],
    )
    .t_end(x_end)
    .build();

    // Create a ODE solver instance
    let h_0: f64 = 0.0001;
    let fac: f64 = 0.9;
    let fac_min: f64 = 0.01;
    let fac_max: f64 = 2.0;
    let n_max: u32 = 800;
    let abs_tol: f64 = 10e-7;
    let rel_tol: f64 = 10e-6;

    let solver: ProportionalControl<f64> =
        ProportionalControl::new(n_max, h_0, fac, fac_min, fac_max, abs_tol, rel_tol);

    // Solve ODE
    let (x, y): (Vec<f64>, Vec<Vector<f64>>) =
        solver.solve(&problem, &DormandPrince54::default()).unwrap();

    //Create chart
    let mut graph_x1: Vec<(f64, f64)> = Vec::with_capacity(x.len());
    let mut graph_x2: Vec<(f64, f64)> = Vec::with_capacity(x.len());
    let mut graph_x3: Vec<(f64, f64)> = Vec::with_capacity(x.len());

    for i in 0..x.len() {
        let x_i = x[i];
        graph_x1.push((x_i, y[i][0]));
        graph_x2.push((x_i, y[i][1]));
        graph_x3.push((x_i, y[i][2]));
    }

    let root_area =
        BitMapBackend::new("./figures/ode_dormandprince.png", (1200, 800)).into_drawing_area();
    root_area.fill(&WHITE).unwrap();

    let mut ctx = ChartBuilder::on(&root_area)
        .margin(20)
        .set_label_area_size(LabelAreaPosition::Left, 40)
        .set_label_area_size(LabelAreaPosition::Bottom, 40)
        .caption("ODE solved with Dormand-Prince", ("Arial", 40))
        .build_cartesian_2d(x_start..x_end, -1.0f64..1.5f64)
        .unwrap();

    ctx.configure_mesh()
        .x_desc("Time t")
        .axis_desc_style(("sans-serif", 25).into_font())
        .draw()
        .unwrap();

    ctx.draw_series(LineSeries::new(graph_x1, &BLACK)).unwrap();

    ctx.draw_series(LineSeries::new(graph_x2, &RED)).unwrap();

    ctx.draw_series(LineSeries::new(graph_x3, &BLUE)).unwrap();
}

The following picture illustrates the solution for this ODE: DormandPrince image